Toepassing van machine learning technieken in het domein van financiën spreekt tot de verbeelding. Welke geheimen liggen verborgen in de data en kunnen met behulp van de juiste analyses naar boven gehaald worden? In deze blog verkennen we met een eerste stap de mogelijkheden van het toepassen van regressie analyse om de variabelen te identificeren die van invloed zijn op het resultaat van een onderneming. De dataset die we hiervoor gebruiken geeft een overzicht per maand van de resultaten en de omzet van die maand. De omzet zal normaal gesproken van grote invloed zijn op het uiteindelijke resultaat.
We maken gebruik van Python voor het uitvoeren van de analyse.
Importeren van de ‘libraries’
Als eerste stap importeren we de libraries numpy en pandas.
[code language=”python”] import numpy as np
import pandas as pd [/dm_code_snippet]
Importeren van de dataset
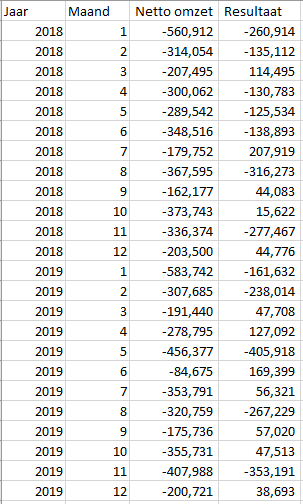
De dataset ziet er als volgt uit:
De dataset wordt ingelezen met behulp van pandas.
[code language=”python”]
dataset = pd.read_csv(‘Dataset.csv’)
X = dataset.iloc[:, 2:-1].values
y = dataset.iloc[:, -1].values
[/dm_code_snippet]
De dataset wordt opgesplitst in twee verschillende onderdelen.
De X dataset bevat de ‘onafhankelijke variabele’ en de y dataset bevat de afhankelijke variabele, de variabele die we willen verklaren.
Voor de eerste analyse kijken we alleen naar de invloed van de Netto omzet en lezen we kolommen Jaar en Maand niet in.
Splitsen van de dataset in een trainings- en een test set
Het is gebruikelijk om de dataset te splitsen in een aparte training dataset en een test dataset. Het machine learning model wordt getraind op basis van de training dataset. De test dataset kan vervolgens worden gebruikt om de betrouwbaarheid van het model te testen.
Voor het splitsen van de dataset maken we gebruik van de library scikit-learn. Scikit-learn is de meest gebruikte library voor machine learning in Python.
[code language=”python”]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
[/dm_code_snippet]
In bovenstaande code wordt een test dataset gemaakt van 20% van de totale dataset.
Trainen van het Simpele Lineaire Regressie model
In onze casus hebben we te maken met één onafhankelijke en één afhankelijke variabele. Met een simpele lineaire regressie kan het verband tussen deze twee variabelen worden gemodelleerd.
Ook hier maken we gebruik van scikit-learn.
[code language=”python”]
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, y_train)
[/dm_code_snippet]
Voorspellen van het resultaat voor de test dataset
Nu we het regressie model getraind hebben, kunnen we nagaan hoe het model het resultaat voorspelt op basis van onze test dataset.
Dit kan met de volgende code:
[code language=”python”]
y_pred = regressor.predict(X_test)
np.set_printoptions(precision=2)
print(np.concatenate((y_pred.reshape(len(y_pred),1), y_test.reshape(len(y_test),1)),1))
[/dm_code_snippet]
Evalueren van de resultaten
Het resultaat van deze code geeft de resultaten van het model:
In de eerste kolom staat de voorspelde waarde door het model. In de tweede kolom is het werkelijke resultaat opgenomen. Voor een aantal waardes benadert het model de werkelijkheid al aardig. Met name de negatieve resultaten liggen echter verder van de werkelijke waarde af.
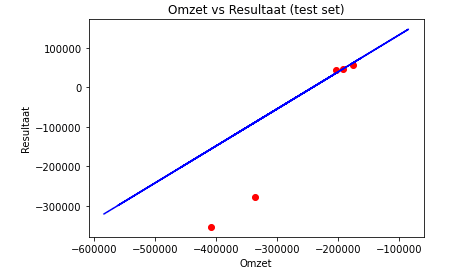
Dit is ook goed te zien in de volgende visualisatie van de resultaten:
Hoe goed het model kan voorspellen (de ‘fit’) kan statistisch gemeten worden met een meetwaarde die R2 wordt genoemd. R2 berekent het deel van de variantie dat wordt verklaard door het statistisch model.
Met de volgende code rekenen we R2 uit voor het huidige model:
[code language=”python”]
from sklearn.metrics import r2_score
r2_score(y_test, y_pred)
[/dm_code_snippet]
Het resultaat van de berekening is:
Iets meer dan de helft van de variantie in het resultaat wordt verklaard door de omzet. Uiteraard kijken we hier slechts naar één variabele en houden we geen rekening met andere variabelen die elkaar ook onderling kunnen beïnvloeden.
De stap naar een Multiple Lineaire Regressie model
Bovenstaand model kunnen we proberen te verbeteren door ook rekening te houden met de andere jaarrekening posten. Hierbij moeten we er wel rekening mee houden dat er een groot verschil kan zitten tussen het minimum en het maximum van de verschillende categorieën. Grote posten hebben daarmee als vanzelfsprekend een grotere invloed op de uitkomst dan de kleinere bedragen. Omdat we willen kijken naar de verklarende waarde van de variantie binnen een categorie, moeten we de waardes eerst ‘schalen’ zodat de waardes ook tussen categorieën vergeleken kunnen worden.
In machine learning termen heet dit ‘feature scaling’.
Met een nieuwe dataset met meer categorieën maken we een nieuw model om te kijken of we daarmee onze performance kunnen verbeteren.
Deze dataset ziet er als volgt uit:
De netto-omzet en het resultaat zijn hetzelfde. We hebben nu echter ook de overige categorieën toegevoegd.
Met de volgende code ‘scalen’ we onze variabelen:
[code language=”python”]
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
sc_y = StandardScaler()
X_train = sc_X.fit_transform(X_train)
y_train = sc_y.fit_transform(y_train)
[/dm_code_snippet]
Als we het model opnieuw op basis van de test dataset de resultaten laten uitrekenen krijgen we een duidelijk ander resultaat:
Op het eerste gezicht lijkt het model nu juist voor de negatieve bedragen beter te voorspellen dan in het vorige model. Wanneer we de R2 berekenen voor het nieuwe model zien we wel een significante verbetering in het aandeel van de variantie die verklaard wordt door ons model.
Conclusie
In deze blog hebben we een eerste verkenning gedaan met de toepassing van machine learning technieken met een financiële dataset. We hebben gebruik gemaakt van een simpele lineaire regressie en een multiple lineaire regressie. Voor nu zijn we voorbijgegaan aan de vraag of de dataset wel voldoet aan de voorwaarden voor lineaire regressie. In de praktijk moet dit uiteraard altijd gevalideerd worden.
De uitkomsten van beide modellen geven nog geen resultaten met een aan zekerheid grenzende waarschijnlijkheid, maar geven al wel een eerste inzicht in de mate waarin de verschillende categorieën het resultaat beïnvloeden. Het biedt in ieder geval een interessante basis voor vervolg analyses.
Meer weten over onze oplossingen?
Onze consultants hebben veel ervaring binnen een grote verscheidenheid aan branches.
Eens verder brainstormen over de mogelijkheden voor jouw organisatie?
Maak kennis met onze specialist Arnoud van der Heiden.